Calculation
Module for calculations and processing of numeric values.
These definitions are part of the calc module and not imported by default. In addition to the functions listed below, the calc module also defines the constants pi, tau, e, and inf.
Functions
abs
Calculates the absolute value of a numeric value.
#calc.abs(-5) \
#calc.abs(5pt - 2cm) \
#calc.abs(2fr) \
#calc.abs(decimal("-342.440"))
value
The value whose absolute value to calculate.
pow
Raises a value to some exponent.
#calc.pow(2, 3) \
#calc.pow(decimal("2.5"), 2)
base
The base of the power.
If this is a decimal, the exponent can only be an integer.
exponent
The exponent of the power.
exp
Raises a value to some exponent of e.
#calc.exp(1)
exponent
The exponent of the power.
sqrt
Calculates the square root of a number.
#calc.sqrt(16) \
#calc.sqrt(2.5)
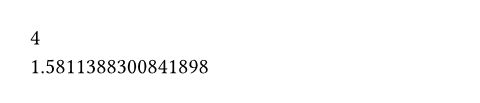
value
The number whose square root to calculate. Must be non-negative.
root
Calculates the real nth root of a number.
If the number is negative, then n must be odd.
#calc.root(16.0, 4) \
#calc.root(27.0, 3)
radicand
The expression to take the root of
index
Which root of the radicand to take
sin
Calculates the sine of an angle.
When called with an integer or a float, they will be interpreted as radians.
#calc.sin(1.5) \
#calc.sin(90deg)
angle
The angle whose sine to calculate.
cos
Calculates the cosine of an angle.
When called with an integer or a float, they will be interpreted as radians.
#calc.cos(1.5) \
#calc.cos(90deg)
angle
The angle whose cosine to calculate.
tan
Calculates the tangent of an angle.
When called with an integer or a float, they will be interpreted as radians.
#calc.tan(1.5) \
#calc.tan(90deg)
angle
The angle whose tangent to calculate.
asin
Calculates the arcsine of a number.
#calc.asin(0) \
#calc.asin(1)
value
The number whose arcsine to calculate. Must be between -1 and 1.
acos
Calculates the arccosine of a number.
#calc.acos(0) \
#calc.acos(1)
value
The number whose arcsine to calculate. Must be between -1 and 1.
atan
Calculates the arctangent of a number.
#calc.atan(0) \
#calc.atan(1)
value
The number whose arctangent to calculate.
atan2
Calculates the four-quadrant arctangent of a coordinate.
The arguments are (x, y), not (y, x).
#calc.atan2(1, 1) \
#calc.atan2(-2, -3)
x
The X coordinate.
y
The Y coordinate.
sinh
Calculates the hyperbolic sine of a hyperbolic angle.
#calc.sinh(0) \
#calc.sinh(1.5)
value
The hyperbolic angle whose hyperbolic sine to calculate.
cosh
Calculates the hyperbolic cosine of a hyperbolic angle.
#calc.cosh(0) \
#calc.cosh(1.5)
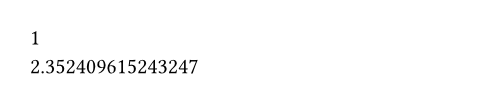
value
The hyperbolic angle whose hyperbolic cosine to calculate.
tanh
Calculates the hyperbolic tangent of an hyperbolic angle.
#calc.tanh(0) \
#calc.tanh(1.5)
value
The hyperbolic angle whose hyperbolic tangent to calculate.
log
Calculates the logarithm of a number.
If the base is not specified, the logarithm is calculated in base 10.
#calc.log(100)
value
The number whose logarithm to calculate. Must be strictly positive.
base
The base of the logarithm. May not be zero.
Default: 10.0
ln
Calculates the natural logarithm of a number.
#calc.ln(calc.e)
value
The number whose logarithm to calculate. Must be strictly positive.
fact
Calculates the factorial of a number.
#calc.fact(5)
number
The number whose factorial to calculate. Must be non-negative.
perm
Calculates a permutation.
Returns the k-permutation of n, or the number of ways to choose k items from a set of n with regard to order.
$ "perm"(n, k) &= n!/((n - k)!) \
"perm"(5, 3) &= #calc.perm(5, 3) $
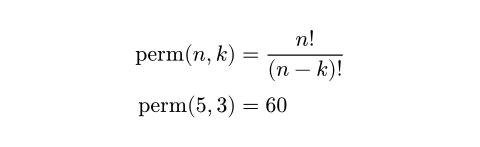
base
The base number. Must be non-negative.
numbers
The number of permutations. Must be non-negative.
binom
Calculates a binomial coefficient.
Returns the k-combination of n, or the number of ways to choose k items from a set of n without regard to order.
#calc.binom(10, 5)
n
The upper coefficient. Must be non-negative.
k
The lower coefficient. Must be non-negative.
gcd
Calculates the greatest common divisor of two integers.
#calc.gcd(7, 42)
a
The first integer.
b
The second integer.
lcm
Calculates the least common multiple of two integers.
#calc.lcm(96, 13)
a
The first integer.
b
The second integer.
floor
Rounds a number down to the nearest integer.
If the number is already an integer, it is returned unchanged.
Note that this function will always return an integer, and will error if the resulting float or decimal is larger than the maximum 64-bit signed integer or smaller than the minimum for that type.
#calc.floor(500.1)
#assert(calc.floor(3) == 3)
#assert(calc.floor(3.14) == 3)
#assert(calc.floor(decimal("-3.14")) == -4)
value
The number to round down.
ceil
Rounds a number up to the nearest integer.
If the number is already an integer, it is returned unchanged.
Note that this function will always return an integer, and will error if the resulting float or decimal is larger than the maximum 64-bit signed integer or smaller than the minimum for that type.
#calc.ceil(500.1)
#assert(calc.ceil(3) == 3)
#assert(calc.ceil(3.14) == 4)
#assert(calc.ceil(decimal("-3.14")) == -3)
value
The number to round up.
trunc
Returns the integer part of a number.
If the number is already an integer, it is returned unchanged.
Note that this function will always return an integer, and will error if the resulting float or decimal is larger than the maximum 64-bit signed integer or smaller than the minimum for that type.
#calc.trunc(15.9)
#assert(calc.trunc(3) == 3)
#assert(calc.trunc(-3.7) == -3)
#assert(calc.trunc(decimal("8493.12949582390")) == 8493)
value
The number to truncate.
fract
Returns the fractional part of a number.
If the number is an integer, returns 0.
#calc.fract(-3.1)
#assert(calc.fract(3) == 0)
#assert(calc.fract(decimal("234.23949211")) == decimal("0.23949211"))
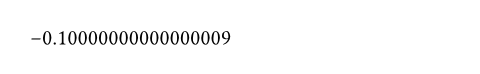
value
The number to truncate.
round
Rounds a number to the nearest integer away from zero.
Optionally, a number of decimal places can be specified.
If the number of digits is negative, its absolute value will indicate the amount of significant integer digits to remove before the decimal point.
Note that this function will return the same type as the operand. That is, applying round to a float will return a float, and to a decimal, another decimal. You may explicitly convert the output of this function to an integer with int, but note that such a conversion will error if the float or decimal is larger than the maximum 64-bit signed integer or smaller than the minimum integer.
In addition, this function can error if there is an attempt to round beyond the maximum or minimum integer or decimal. If the number is a float, such an attempt will cause float.inf or -float.inf to be returned for maximum and minimum respectively.
#calc.round(3.1415, digits: 2)
#assert(calc.round(3) == 3)
#assert(calc.round(3.14) == 3)
#assert(calc.round(3.5) == 4.0)
#assert(calc.round(3333.45, digits: -2) == 3300.0)
#assert(calc.round(-48953.45, digits: -3) == -49000.0)
#assert(calc.round(3333, digits: -2) == 3300)
#assert(calc.round(-48953, digits: -3) == -49000)
#assert(calc.round(decimal("-6.5")) == decimal("-7"))
#assert(calc.round(decimal("7.123456789"), digits: 6) == decimal("7.123457"))
#assert(calc.round(decimal("3333.45"), digits: -2) == decimal("3300"))
#assert(calc.round(decimal("-48953.45"), digits: -3) == decimal("-49000"))
value
The number to round.
digits
If positive, the number of decimal places.
If negative, the number of significant integer digits that should be removed before the decimal point.
Default: 0
clamp
Clamps a number between a minimum and maximum value.
#calc.clamp(5, 0, 4)
#assert(calc.clamp(5, 0, 10) == 5)
#assert(calc.clamp(5, 6, 10) == 6)
#assert(calc.clamp(decimal("5.45"), 2, decimal("45.9")) == decimal("5.45"))
#assert(calc.clamp(decimal("5.45"), decimal("6.75"), 12) == decimal("6.75"))
value
The number to clamp.
min
The inclusive minimum value.
max
The inclusive maximum value.
min
Determines the minimum of a sequence of values.
#calc.min(1, -3, -5, 20, 3, 6) \
#calc.min("typst", "is", "cool")
valuesanyRequiredPositionalVariadic
The sequence of values from which to extract the minimum. Must not be empty.
max
Determines the maximum of a sequence of values.
#calc.max(1, -3, -5, 20, 3, 6) \
#calc.max("typst", "is", "cool")
valuesanyRequiredPositionalVariadic
The sequence of values from which to extract the maximum. Must not be empty.
even
Determines whether an integer is even.
#calc.even(4) \
#calc.even(5) \
#range(10).filter(calc.even)
value
The number to check for evenness.
odd
Determines whether an integer is odd.
#calc.odd(4) \
#calc.odd(5) \
#range(10).filter(calc.odd)
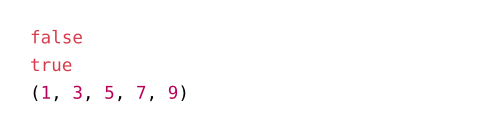
value
The number to check for oddness.
rem
Calculates the remainder of two numbers.
The value calc.rem(x, y) always has the same sign as x, and is smaller in magnitude than y.
This can error if given a decimal input and the dividend is too small in magnitude compared to the divisor.
#calc.rem(7, 3) \
#calc.rem(7, -3) \
#calc.rem(-7, 3) \
#calc.rem(-7, -3) \
#calc.rem(1.75, 0.5)
dividend
The dividend of the remainder.
divisor
The divisor of the remainder.
div-euclid
Performs euclidean division of two numbers.
The result of this computation is that of a division rounded to the integer n such that the dividend is greater than or equal to n times the divisor.
#calc.div-euclid(7, 3) \
#calc.div-euclid(7, -3) \
#calc.div-euclid(-7, 3) \
#calc.div-euclid(-7, -3) \
#calc.div-euclid(1.75, 0.5) \
#calc.div-euclid(decimal("1.75"), decimal("0.5"))
dividend
The dividend of the division.
divisor
The divisor of the division.
rem-euclid
This calculates the least nonnegative remainder of a division.
Warning: Due to a floating point round-off error, the remainder may equal the absolute value of the divisor if the dividend is much smaller in magnitude than the divisor and the dividend is negative. This only applies for floating point inputs.
In addition, this can error if given a decimal input and the dividend is too small in magnitude compared to the divisor.
#calc.rem-euclid(7, 3) \
#calc.rem-euclid(7, -3) \
#calc.rem-euclid(-7, 3) \
#calc.rem-euclid(-7, -3) \
#calc.rem-euclid(1.75, 0.5) \
#calc.rem-euclid(decimal("1.75"), decimal("0.5"))
dividend
The dividend of the remainder.
divisor
The divisor of the remainder.
quo
Calculates the quotient (floored division) of two numbers.
Note that this function will always return an integer, and will error if the resulting float or decimal is larger than the maximum 64-bit signed integer or smaller than the minimum for that type.
$ "quo"(a, b) &= floor(a/b) \
"quo"(14, 5) &= #calc.quo(14, 5) \
"quo"(3.46, 0.5) &= #calc.quo(3.46, 0.5) $
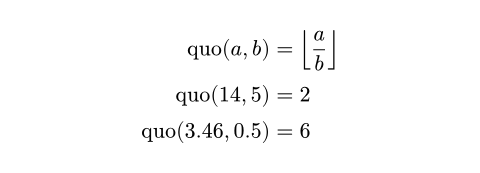
dividend
The dividend of the quotient.
divisor
The divisor of the quotient.